Matematičko očekivanje je definicija
Čeka se mat jedan od najvažnijih koncepata u matematičkoj statistici i teoriji vjerojatnosti, koji karakterizira distribuciju vrijednosti ili vjerovatnoće slučajna varijabla. Obično se izražava kao ponderisani prosjek svih mogućih parametara slučajne varijable. Široko se koristi u tehničkoj analizi, proučavanju nizova brojeva i proučavanju kontinuiranih i dugotrajnih procesa. Važan je u procjeni rizika, predviđanju indikatora cijena prilikom trgovanja na finansijskim tržištima, a koristi se u razvoju strategija i metoda igračkih taktika u teorije kockanja.
Šah-mat čeka- Ovo srednja vrijednost slučajne varijable, distribucija vjerovatnoće slučajna varijabla se razmatra u teoriji vjerovatnoće.
Čeka se mat mjera prosječne vrijednosti slučajne varijable u teoriji vjerovatnoće. Matirajte očekivanje slučajne varijable x označeno sa M(x).
Matematičko očekivanje (srednja populacija) je
Čeka se mat

Čeka se mat u teoriji vjerovatnoće, ponderisani prosjek svih mogućih vrijednosti koje slučajna varijabla može uzeti.

Čeka se mat zbir proizvoda svih mogućih vrijednosti slučajne varijable i vjerovatnoće tih vrijednosti.
Matematičko očekivanje (srednja populacija) je
Čeka se mat prosječna korist od određene odluke, pod uslovom da se takva odluka može razmatrati u okviru teorije velikih brojeva i velike udaljenosti.

Čeka se mat u teoriji kockanja, iznos dobitka koji špekulant može zaraditi ili izgubiti, u prosjeku, na svaku opkladu. Jezikom kockanja špekulanti ovo se ponekad naziva "prednošću" špekulant" (ako je pozitivna za špekulanta) ili "kućna ivica" (ako je negativna za špekulanta).
Matematičko očekivanje (srednja populacija) je
Čeka se mat profit po pobjedi pomnožen prosjekom profit, minus gubitak, pomnožen sa prosječnim gubitkom.

Matematičko očekivanje slučajne varijable u matematičkoj teoriji
Jedna od važnih numeričkih karakteristika slučajne varijable je očekivana vrijednost. Hajde da uvedemo koncept sistema slučajnih varijabli. Razmotrimo skup slučajnih varijabli koje su rezultati istog slučajnog eksperimenta. Ako je jedna od mogućih vrijednosti sistema, onda događaj odgovara određenoj vjerovatnoći koja zadovoljava Kolmogorovljeve aksiome. Funkcija definirana za sve moguće vrijednosti slučajnih varijabli naziva se zajednički zakon distribucije. Ova funkcija vam omogućava da izračunate vjerovatnoće bilo kojeg događaja iz. Konkretno, joint zakon distribucije slučajnih varijabli i, koje uzimaju vrijednosti iz skupa i, date su vjerovatnoćama.

Termin "mat. očekivanje“ uveo je Pierre Simon Marquis de Laplace (1795) i potiče od koncepta „očekivana vrijednost dobitka“, koji se prvi put pojavio u 17. stoljeću u teoriji kockanja u djelima Blaisea Pascal-a i Christiaana Huygensa. Međutim, prvo potpuno teorijsko razumijevanje i ocjenu ovog koncepta dao je Pafnuti Lvovič Čebišev (sredina 19. stoljeća).

Zakon distribucije slučajnih numeričkih varijabli (funkcija distribucije i serija distribucije ili gustina vjerovatnoće) u potpunosti opisuju ponašanje slučajne varijable. Ali u nizu problema dovoljno je poznavati neke numeričke karakteristike veličine koja se proučava (na primjer, njenu prosječnu vrijednost i moguće odstupanje od nje) da bi se odgovorilo na postavljeno pitanje. Glavne numeričke karakteristike slučajnih varijabli su očekivanje, varijansa, mod i medijan.
Očekivana vrijednost diskretne slučajne varijable je zbir proizvoda njenih mogućih vrijednosti i njihovih odgovarajućih vjerovatnoća. Ponekad psovke. očekivanje se naziva ponderisanim prosjekom, jer je približno jednako aritmetičkoj sredini promatranih vrijednosti slučajne varijable u velikom broju eksperimenata. Iz definicije vrijednosti očekivanja slijedi da njena vrijednost nije manja od najmanje moguće vrijednosti slučajne varijable i ne veća od najveće. Očekivana vrijednost slučajne varijable je neslučajna (konstantna) varijabla.

Matematičko očekivanje ima jednostavno fizičko značenje: ako stavite jediničnu masu na pravu liniju, stavite određenu masu u neke tačke (za diskretnu distribuciju) ili je "razmažete" određenom gustinom (za apsolutno kontinuiranu distribuciju) , tada će tačka koja odgovara matematičkom očekivanju biti koordinata "centar gravitacije" ravna.

Prosječna vrijednost slučajne varijable je određeni broj koji je, takoreći, njen „predstavnik“ i zamjenjuje ga u približno približnim proračunima. Kada kažemo: "prosječno vrijeme rada lampe je 100 sati" ili "prosječna tačka udara je pomjerena u odnosu na metu za 2 m udesno", ukazujemo na određenu numeričku karakteristiku slučajne varijable koja opisuje njenu lokaciju. na numeričkoj osi, tj. "karakteristike položaja".
Među karakteristikama pozicije u teoriji vjerovatnoće, najvažniju ulogu igra očekivana vrijednost slučajne varijable, koja se ponekad naziva jednostavno prosječnom vrijednošću slučajne varijable.

Uzmite u obzir slučajnu varijablu X, sa mogućim vrijednostima x1, x2, …, xn sa vjerovatnoćama p1, p2, …, pn. Moramo nekim brojem okarakterizirati položaj vrijednosti slučajne varijable na osi apscise sa uzimajući u obzir da ove vrijednosti imaju različite vjerovatnoće. U tu svrhu, prirodno je koristiti takozvani „ponderisani prosek“ vrednosti xi, a svaku vrijednost xi tokom usrednjavanja treba uzeti u obzir sa “težinom” proporcionalnom vjerovatnoći ove vrijednosti. Stoga ćemo izračunati prosjek slučajne varijable X, koje označavamo M |X|:

Ovaj ponderisani prosjek naziva se očekivana vrijednost slučajne varijable. Tako smo uveli u razmatranje jedan od najvažnijih koncepata teorije vjerovatnoće – koncept matematike. očekivanja. Mat. Očekivanje slučajne varijable je zbir proizvoda svih mogućih vrijednosti slučajne varijable i vjerovatnoća tih vrijednosti.
Mat. čeka na slučajnu varijablu X je povezan osebujnom zavisnošću sa aritmetičkom sredinom posmatranih vrednosti slučajne varijable u velikom broju eksperimenata. Ova zavisnost je istog tipa kao i zavisnost između učestalosti i verovatnoće, naime: kod velikog broja eksperimenata, aritmetička sredina posmatranih vrednosti slučajne varijable približava se (konvergira u verovatnoći) njenoj matematici. čekanje. Iz prisustva veze između frekvencije i vjerovatnoće, može se zaključiti kao posljedica prisutnosti slične veze između aritmetičke sredine i matematičkog očekivanja. Zaista, razmotrite slučajnu varijablu X, karakteriziran distribucijskim nizom:

Neka se proizvede N nezavisni eksperimenti, u svakom od kojih vrijednost X poprima određenu vrijednost. Pretpostavimo da je vrijednost x1 pojavio m1 vremena, vrijednost x2 pojavio m2 jednom, u opštem smislu xi pojavio mi se puta. Izračunajmo aritmetičku sredinu uočenih vrijednosti vrijednosti X, koja je, za razliku od matematičkog očekivanja M|X| označavamo M*|X|:
Sa povećanjem broja eksperimenata N frekvencije piće se približiti (konvergirati u vjerovatnoći) odgovarajućim vjerovatnoćama. Posljedično, aritmetička sredina promatranih vrijednosti slučajne varijable M|X| sa povećanjem broja eksperimenata će se približiti (konvergirati u vjerovatnoći) svojoj očekivanoj vrijednosti. Gore formulisana veza između aritmetičke sredine i matematike. očekivanje je sadržaj jednog od oblika zakona velikih brojeva.
Već znamo da svi oblici zakona velikih brojeva navode činjenicu da su neki prosjeci stabilni u velikom broju eksperimenata. Ovdje govorimo o stabilnosti aritmetičke sredine iz serije opažanja iste veličine. Uz mali broj eksperimenata, aritmetička sredina njihovih rezultata je slučajna; s dovoljnim povećanjem broja eksperimenata, postaje "gotovo neslučajan" i, stabilizirajući se, približava se konstantnoj vrijednosti - mat. čekanje.

Stabilnost prosjeka u velikom broju eksperimenata može se lako eksperimentalno provjeriti. Na primjer, kada vagamo tijelo u laboratoriju na preciznoj vagi, kao rezultat vaganja svaki put dobijamo novu vrijednost; Da bismo smanjili grešku u promatranju, tijelo izmjerimo nekoliko puta i koristimo aritmetičku sredinu dobivenih vrijednosti. Lako je uočiti da daljim povećanjem broja eksperimenata (vaganja) aritmetička sredina sve manje reaguje na to povećanje i, uz dovoljno veliki broj eksperimenata, praktično prestaje da se menja.
Treba napomenuti da je najvažnija karakteristika položaja slučajne varijable mat. očekivanje - ne postoji za sve slučajne varijable. Moguće je kreirati primjere takvih slučajnih varijabli za koje mat. nema očekivanja jer se odgovarajući zbir ili integral divergiraju. Međutim, takvi slučajevi nisu od značajnog interesa za praksu. Tipično, slučajne varijable s kojima se bavimo imaju ograničen raspon mogućih vrijednosti i, naravno, imaju matematička očekivanja.

Pored najvažnije od karakteristika položaja slučajne varijable - očekivane vrijednosti - u praksi se ponekad koriste i druge karakteristike pozicije, posebno mod i medijan slučajne varijable.

Mod slučajne varijable je njena najvjerovatnija vrijednost. Izraz "najvjerovatnija vrijednost" striktno govoreći primjenjuje se samo na diskontinuirane količine; za kontinuiranu količinu, mod je vrijednost pri kojoj je gustina vjerovatnoće maksimalna. Slike pokazuju način rada za diskontinuirane i kontinuirane slučajne varijable, respektivno.

Ako poligon distribucije (kriva distribucije) ima više od jednog maksimuma, distribucija se naziva "multimodalna".


Ponekad postoje distribucije koje imaju minimum u sredini, a ne maksimum. Takve distribucije se nazivaju „antimodalne“.

U opštem slučaju, mod i očekivana vrednost slučajne varijable se ne poklapaju. U posebnom slučaju kada je distribucija simetrična i modalna (tj. ima mod) i postoji mat. očekivanje, onda se poklapa sa modom i centrom simetrije distribucije.
Često se koristi još jedna karakteristika pozicije - takozvani medijan slučajne varijable. Ova karakteristika se obično koristi samo za kontinuirane slučajne varijable, iako se formalno može definirati za diskontinuiranu varijablu. Geometrijski gledano, medijana je apscisa tačke u kojoj je područje zatvoreno krivom raspodjele podijeljeno na pola.

U slučaju simetrične modalne distribucije, medijana se poklapa sa mat. očekivanja i mode.
Očekivana vrijednost je prosječna vrijednost slučajne varijable - numerička karakteristika distribucije vjerovatnoće slučajne varijable. Na najopštiji način, matirajte očekivanje slučajne varijable X(w) je definisan kao Lebesgueov integral u odnosu na mjeru vjerovatnoće R u izvornom prostoru vjerovatnoće:

Mat. očekivanje se također može izračunati kao Lebesgueov integral od X po distribuciji vjerovatnoće px količine X:

Prirodno je definisati koncept slučajne varijable sa beskonačnim očekivanjem. Tipičan primjer su vremena repatrijacije u nekim slučajnim šetnjama.
Uz pomoć prostirke. očekivanja definiraju mnoge numeričke i funkcionalne karakteristike distribucije (kao matematičko očekivanje odgovarajućih funkcija od slučajne varijable), na primjer, generirajuća funkcija, karakteristična funkcija, momenti bilo kojeg reda, posebno disperzija, kovarijansa.
Matematičko očekivanje (srednja populacija) je
Matematičko očekivanje je karakteristika lokacije vrijednosti slučajne varijable (prosječne vrijednosti njene distribucije). U tom svojstvu, matematičko očekivanje služi kao neki „tipični“ parametar distribucije i njegova uloga je slična ulozi statičkog momenta – koordinate težišta distribucije mase – u mehanici. Očekivanje se razlikuje od ostalih lokacijskih karakteristika uz pomoć kojih se distribucija opisuje općenito - medijani, modovi, matovi - po većoj vrijednosti koju ono i odgovarajuća karakteristika raspršenja - disperzija - imaju u graničnim teoremama teorije vjerovatnoće. Značenje mate očekivanja najpotpunije otkriva zakon velikih brojeva (Čebiševljeva nejednakost) i pojačani zakon velikih brojeva.
Matematičko očekivanje (srednja populacija) je
Očekivanje diskretne slučajne varijable
Neka postoji neka slučajna varijabla koja može uzeti jednu od nekoliko numeričkih vrijednosti (na primjer, broj bodova pri bacanju kocke može biti 1, 2, 3, 4, 5 ili 6). Često se u praksi, za takvu vrijednost, postavlja pitanje: koju vrijednost uzima "u prosjeku" s velikim brojem testova? Koliki će biti naš prosječni prihod (ili gubitak) od svake od rizičnih transakcija?

Recimo da postoji neka vrsta lutrije. Želimo da shvatimo da li je isplativo ili ne učestvovati u tome (ili čak učestvovati više puta, redovno). Recimo da je svaka četvrta karta pobjednička, nagrada će biti 300 rubalja, a svaka karta će biti 100 rubalja. Uz beskonačno veliki broj učešća, evo šta se dešava. U tri četvrtine slučajeva ćemo izgubiti, svaka tri gubitka koštat će 300 rubalja. U svakom četvrtom slučaju dobit ćemo 200 rubalja. (nagrada minus trošak), to jest, za četiri učešća gubimo u prosjeku 100 rubalja, za jedno - u prosjeku 25 rubalja. Ukupno, prosječna cijena naše ruševine bit će 25 rubalja po karti.
Bacamo kockice. Ako nije varanje (bez pomeranja centra gravitacije, itd.), koliko ćemo onda u proseku imati poena u jednom trenutku? Pošto je svaka opcija jednako vjerovatna, jednostavno uzimamo aritmetičku sredinu i dobijemo 3,5. Pošto je ovo PROSEK, nema potrebe da se ljutite što ni jedno konkretno bacanje neće dati 3,5 poena - pa ova kocka nema lice sa takvim brojem!
Sada da sumiramo naše primjere:

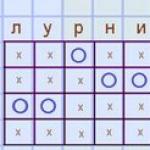
Pogledajmo upravo datu sliku. Na lijevoj strani je tabela distribucije slučajne varijable. Vrijednost X može uzeti jednu od n mogućih vrijednosti (prikazano u gornjem redu). Ne može postojati nikakva druga značenja. Ispod svake moguće vrijednosti je njena vjerovatnoća. Na desnoj strani je formula, gdje se M(X) naziva mat. čekanje. Značenje ove vrijednosti je da će s velikim brojem testova (sa velikim uzorkom) prosječna vrijednost težiti istom očekivanju.
Vratimo se ponovo na istu kocku za igru. Mat. očekivani broj poena pri bacanju je 3,5 (izračunajte sami koristeći formulu ako mi ne vjerujete). Recimo da ste ga bacili nekoliko puta. Rezultati su bili 4 i 6. Prosek je bio 5, što je daleko od 3,5. Bacili su ga još jednom, dobili su 3, odnosno u prosjeku (4 + 6 + 3)/3 = 4,3333... Nekako daleko od strunjače. očekivanja. Sada napravite ludi eksperiment - okrenite kocku 1000 puta! A čak i da prosek nije tačno 3,5, biće blizu toga.
Izračunajmo prostirku. čekaju gore opisanu lutriju. Ploča će izgledati ovako:

Tada će očekivanje mat-a biti kao što smo utvrdili gore:
Druga stvar je da bi bilo teško to učiniti "na prste" bez formule da postoji više opcija. Pa, recimo da bi bilo 75% izgubljenih tiketa, 20% dobitnih tiketa i 5% posebno dobitnih.
Sada neke nekretnine ispunjavaju očekivanja.
Mat. očekivanje je linearno. Lako je dokazati:

Konstantni množitelj se može izvaditi izvan znaka mat. očekivanja, odnosno:
Ovo je poseban slučaj svojstva linearnosti mate očekivanja.
Još jedna posljedica linearnosti mat. očekivanja:
odnosno mat. očekivanje sume slučajnih varijabli je jednako zbiru matematičkih očekivanja slučajnih varijabli.
Neka su X, Y nezavisne slučajne varijable, Zatim:
Ovo je takođe lako dokazati) Rad XY sama po sebi je slučajna varijabla, i ako bi početne vrijednosti mogle poprimiti n I m vrijednosti prema tome XY može uzeti nm vrijednosti. svaka vrijednost se izračunava na osnovu činjenice da se vjerovatnoće nezavisnih događaja množe. Kao rezultat, dobijamo ovo:

Očekivanje kontinuirane slučajne varijable
Kontinuirane slučajne varijable imaju takvu karakteristiku kao što je gustina distribucije (gustina vjerovatnoće). U suštini karakteriše situaciju da slučajna varijabla češće uzima neke vrijednosti iz skupa realnih brojeva, a neke rjeđe. Na primjer, razmotrite ovaj grafikon:

Evo X- stvarna slučajna varijabla, f(x)- gustina distribucije. Sudeći po ovom grafikonu, tokom eksperimenata vrijednost Xčesto će biti broj blizu nule. Šanse su premašene 3 ili biti manji -3 prilično čisto teorijski.
Ako je gustina distribucije poznata, onda se očekivana vrijednost nalazi na sljedeći način:

Neka, na primjer, postoji uniformna raspodjela:

Hajde da nađemo mat. očekivanje:

Ovo je sasvim u skladu s intuitivnim razumijevanjem. Recimo, ako dobijemo mnogo slučajnih realnih brojeva sa uniformnom distribucijom, svaki segment |0; 1| , tada bi aritmetička sredina trebala biti oko 0,5.
Svojstva matematičkih očekivanja - linearnost, itd., primenljiva za diskretne slučajne varijable, takođe su primenljiva ovde.
Odnos između matematičkog očekivanja i drugih statističkih pokazatelja
IN statistički analiza, uz matematičko očekivanje, postoji sistem međuzavisnih indikatora koji odražavaju homogenost pojava i stabilnost procesi. Indikatori varijacije često nemaju nezavisno značenje i koriste se za dalju analizu podataka. Izuzetak je koeficijent varijacije, koji karakteriše homogenost podacišta je vredno statistički karakteristika.

Stepen varijabilnosti ili stabilnosti procesi u statističkoj nauci može se mjeriti korištenjem nekoliko indikatora.
Najvažniji indikator koji karakteriše varijabilnost slučajna varijabla je Disperzija, što je najbliže i direktno povezano sa mat. čekanje. Ovaj parametar se aktivno koristi u drugim vrstama statističkih analiza (testiranje hipoteza, analiza uzročno-posljedičnih veza, itd.). Kao i prosječno linearno odstupanje, disperzija također odražava mjeru širenja podaci oko prosječne vrijednosti.

Korisno je prevesti jezik znakova u jezik riječi. Ispada da je disperzija prosječan kvadrat odstupanja. Odnosno, prvo se izračunava prosječna vrijednost, zatim se uzima razlika između svake izvorne i prosječne vrijednosti, kvadrira, dodaje, a zatim dijeli sa brojem vrijednosti u populaciji. Razlika između pojedinačne vrijednosti i prosjeka odražava mjeru odstupanja. Kvadira se tako da sva odstupanja postanu isključivo pozitivni brojevi i kako bi se izbjeglo međusobno uništavanje pozitivnih i negativnih devijacija prilikom njihovog sabiranja. Zatim, s obzirom na kvadratna odstupanja, jednostavno izračunamo aritmetičku sredinu. Srednja kvadratna odstupanja. Odstupanja se kvadriraju i izračunava se prosjek. Odgovor na magičnu reč "disperzija" leži u samo tri reči.
Međutim, u svom čistom obliku, kao što je aritmetička sredina ili disperzija, se ne koristi. To je prije pomoćni i srednji indikator koji se koristi za druge vrste statističkih analiza. Čak nema ni normalnu mjernu jedinicu. Sudeći po formuli, ovo je kvadrat mjerne jedinice izvornih podataka.
Matematičko očekivanje (srednja populacija) je
Izmjerimo slučajnu varijablu N puta, na primjer, mjerimo brzinu vjetra deset puta i želimo pronaći prosječnu vrijednost. Kako je prosječna vrijednost povezana sa funkcijom distribucije?
Ili ćemo baciti kockice veliki broj puta. Broj bodova koji će se pojaviti na kocki sa svakim bacanjem je slučajna varijabla i može uzeti bilo koju prirodnu vrijednost od 1 do 6. Aritmetička sredina ispuštenih bodova izračunata za sva bacanja je također slučajna varijabla, ali za velike N teži vrlo specifičnom broju - mat. čekanje Mx. U ovom slučaju Mx = 3,5.
Kako ste dobili ovu vrijednost? Pusti unutra N testovi n1 kada dobijete 1 bod, n2 jednom - 2 boda i tako dalje. Zatim broj ishoda u koji je pao jedan bod:

Slično za ishode kada se bacaju 2, 3, 4, 5 i 6 poena.

Pretpostavimo sada da znamo distribuciju slučajne varijable x, odnosno znamo da slučajna varijabla x može poprimiti vrijednosti x1, x2,..., xk sa vjerovatnoćama p1, p2,..., pk .
Matematičko očekivanje Mx slučajne varijable x je jednako:

Matematičko očekivanje nije uvijek razumna procjena neke slučajne varijable. Dakle, za procjenu prosječne plate razumnije je koristiti koncept medijane, odnosno takve vrijednosti da broj ljudi koji zarađuju manji od medijane plata i veliki, poklapaju se.
Vjerovatnoća p1 da će slučajna varijabla x biti manja od x1/2 i vjerovatnoća p2 da će slučajna varijabla x biti veća od x1/2, iste su i jednake su 1/2. Medijan nije određen jedinstveno za sve distribucije.

Standardna ili standardna devijacija u statistici se naziva stepen odstupanja opservacijskih podataka ili skupova od PROSJEČNE vrijednosti. Označava se slovima s ili s. Mala standardna devijacija ukazuje da se podaci grupišu oko srednje vrednosti, dok velika standardna devijacija ukazuje da se početni podaci nalaze daleko od nje. Standardna devijacija jednaka je kvadratnom korijenu veličine koja se zove varijansa. To je prosjek zbira kvadrata razlika početnih podataka koji odstupaju od prosječne vrijednosti. Standardna devijacija slučajne varijable je kvadratni korijen varijanse:

Primjer. U uslovima testiranja kada pucate na metu, izračunajte disperziju i standardnu devijaciju slučajne varijable:

Varijacija- fluktuacija, promjenjivost vrijednosti neke karakteristike među jedinicama stanovništva. Pojedinačne numeričke vrijednosti neke karakteristike pronađene u populaciji koja se proučava nazivaju se varijantne vrijednosti. Nedovoljnost prosječne vrijednosti za potpunu karakterizaciju populacije prisiljava nas da prosječne vrijednosti dopunimo indikatorima koji nam omogućavaju da procijenimo tipičnost ovih prosjeka mjerenjem varijabilnosti (varijacije) karakteristike koja se proučava. Koeficijent varijacije se izračunava pomoću formule:

Raspon varijacija(R) predstavlja razliku između maksimalne i minimalne vrijednosti atributa u populaciji koja se proučava. Ovaj pokazatelj daje najopćenitiju ideju o varijabilnosti karakteristike koja se proučava, kao što pokazuje razlika samo između ekstremnih vrijednosti opcija. Ovisnost o ekstremnim vrijednostima karakteristike daje opsegu varijacije nestabilan, slučajan karakter.

Prosječna linearna devijacija predstavlja aritmetičku sredinu apsolutnih (modulo) odstupanja svih vrijednosti analizirane populacije od njihove prosječne vrijednosti:

Očekivanje u teoriji kockanja
Čeka se mat prosječan iznos novca koji špekulant kockanja može dobiti ili izgubiti na datu opkladu. Ovo je vrlo važan koncept za špekulanta jer je od suštinskog značaja za procjenu većine kockarskih situacija. Šah-mat je također optimalan alat za analizu osnovnih rasporeda kartica i situacija u igri.
Recimo da igrate igru novčića sa prijateljem, kladite se na 1 dolar svaki put, bez obzira šta se pojavi. Rep znači da pobjeđuješ, glava gubi. Šanse su jedan prema jedan da će se pojaviti, tako da se kladite $1 prema $1. Dakle, vaše očekivanje za mat je jednako nuli, jer Sa matematičke tačke gledišta, ne možete znati da li ćete voditi ili izgubiti nakon dva bacanja ili nakon 200.

Vaš dobitak po satu je nula. Dobici po satu su iznos novca koji očekujete da ćete osvojiti za sat vremena. Možete baciti novčić 500 puta za sat vremena, ali nećete pobijediti ili izgubiti jer... Vaše šanse nisu ni pozitivne ni negativne. Sa tačke gledišta ozbiljnog špekulanta, ovaj sistem klađenja nije loš. Ali ovo je jednostavno gubljenje vremena.
Ali recimo da neko želi da se kladi 2$ protiv vašeg 1$ u istoj igri. Tada odmah imate pozitivno očekivanje od 50 centi od svake opklade. Zašto 50 centi? U prosjeku dobijete jednu opkladu i izgubite drugu. Kladite se prvo i izgubit ćete 1$, kladite se drugi i dobit ćete 2$. Kladite se dva puta po $1 i imate prednost od $1. Dakle, svaka vaša opklada na jedan dolar dala vam je 50 centi.

Ako se novčić pojavi 500 puta u jednom satu, vaš dobitak po satu će već biti 250 dolara, jer... u prosjeku ste izgubili jednu dolar 250 puta i osvojio dva dolar 250 puta. 500$ minus 250$ je 250$, što je ukupan dobitak. Imajte na umu da je očekivana vrijednost, koja je prosječan iznos koji dobijete po opkladi, 50 centi. Osvojili ste 250 dolara kladeći se na dolar 500 puta, što je jednako 50 centi po opkladi.
Matematičko očekivanje (srednja populacija) je
Mat. čekanje nema veze sa kratkoročnim rezultatima. Vaš protivnik, koji je odlučio da kladi 2$ protiv vas, mogao bi vas pobijediti na prvih deset bacanja zaredom, ali vi, ako imate prednost u klađenju od 2 prema 1, pod svim ostalim jednakim uvjetima, zaradit ćete 50 centi na svaki $1 opkladu u bilo kojoj okolnosti. Nije bitno hoćete li dobiti ili izgubiti jednu ili nekoliko opklada, sve dok imate dovoljno novca da udobno pokrijete troškove. Ako nastavite da se kladite na isti način, tada će se tokom dužeg vremenskog perioda vaš dobitak približiti zbroju očekivanja u pojedinačnim bacanjima.

Svaki put kada napravite najbolju opkladu (opkladu koja se može pokazati isplativom na duge staze), kada su kvote u vašu korist, obavezno ćete nešto osvojiti na tome, bez obzira da li to izgubite ili ne u data hand. Suprotno tome, ako napravite underdog opkladu (opkladu koja je neisplativa na duge staze) kada su šanse protiv vas, gubite nešto bez obzira na to da li dobijete ili izgubite ruku.
Matematičko očekivanje (srednja populacija) je
Stavljate opkladu sa najboljim ishodom ako su vaša očekivanja pozitivna, a pozitivna je ako su kvote na vašoj strani. Kada položite opkladu sa najgorim ishodom, imate negativna očekivanja, što se dešava kada su kvote protiv vas. Ozbiljni špekulanti se klade samo na najbolji ishod, ako se dogodi najgori, odustaju. Šta šanse znače u vašu korist? Možda ćete na kraju osvojiti više nego što donose stvarne kvote. Prave šanse za sletanje su 1 prema 1, ali dobijate 2 prema 1 zbog omjera izgleda. U ovom slučaju, šanse su u vašu korist. Definitivno ćete dobiti najbolji ishod uz pozitivno očekivanje od 50 centi po opkladi.

Evo složenijeg primjera prostirke. očekivanja. Prijatelj zapisuje brojeve od jedan do pet i kladi se $5 protiv vašeg $1 da nećete pogoditi broj. Treba li pristati na takvu opkladu? Šta se tu očekuje?
U prosjeku ćete pogriješiti četiri puta. Na osnovu toga, šanse protiv toga da pogodite broj su 4 prema 1. Šanse protiv toga da izgubite dolar u jednom pokušaju. Međutim, dobijate 5 prema 1, uz mogućnost gubitka 4 prema 1. Dakle, kvote su u vašu korist, možete uzeti opkladu i nadati se najboljem ishodu. Ako uložite ovu opkladu pet puta, u prosjeku ćete četiri puta izgubiti 1$ i jednom dobiti 5$. Na osnovu toga, za svih pet pokušaja ćete zaraditi 1 dolar uz pozitivno matematičko očekivanje od 20 centi po opkladi.

Špekulant koji očekuje da će dobiti više nego što se kladi, kao u gornjem primjeru, riskira. Naprotiv, on uništava svoje šanse kada očekuje da će dobiti manje nego što se kladi. Špekulant koji se kladi može imati pozitivna ili negativna očekivanja, što zavisi od toga da li dobija ili uništava kvote.
Ako se kladite na $50 da osvojite $10 sa šansom za pobjedu 4 prema 1, dobit ćete negativno očekivanje od $2 jer U prosjeku ćete četiri puta osvojiti 10 dolara i jednom izgubiti 50 dolara, što pokazuje da će gubitak po opkladi biti 10 dolara. Ali ako se kladite na 30 dolara da dobijete 10 dolara, sa istim izgledima za pobjedu 4 prema 1, tada u ovom slučaju imate pozitivno očekivanje od 2 dolara, jer ponovo dobijate četiri puta po 10$ i gubite jednom 30$, što je profit po $10. Ovi primjeri pokazuju da je prva opklada loša, a druga dobra.

Mat. anticipacija je centar svake situacije u igri. Kada kladionica ohrabruje ljubitelje fudbala da se klade na 11 dolara da dobiju 10 dolara, on ima pozitivno očekivanje od 50 centi na svakih 10 dolara. Ako kazino isplati čak i novac sa linije za prolaz u kockovima, tada će pozitivna očekivanja kazina biti otprilike 1,40 dolara za svakih 100 dolara, jer Ova igra je strukturirana tako da svako ko se kladi na ovu liniju gubi u prosjeku 50,7% i dobije 49,3% ukupnog vremena. Bez sumnje, upravo ovo naizgled minimalno pozitivno očekivanje donosi kolosalan profit vlasnicima kazina širom svijeta. Kako je primetio vlasnik kazina Vegas World Bob Stupak, „hiljaditi posto negativna vjerovatnoća na dovoljno velikoj udaljenosti uništit će najbogatijeg čovjeka na svijetu.”

Očekivanje kada igrate poker
Igra pokera je najilustrativniji i najilustrativniji primjer sa stanovišta korištenja teorije i svojstava partnera očekivanja.

Mat. Očekivana vrijednost u pokeru je prosječna korist od određene odluke, pod uslovom da se takva odluka može razmatrati u okviru teorije velikih brojeva i velike udaljenosti. Uspješna poker igra je uvijek prihvatiti poteze sa pozitivnom očekivanom vrijednošću.
Matematičko očekivanje (srednja populacija) je
Matematičko značenje matematike. Očekivanje pri igranju pokera je da se često susrećemo sa slučajnim varijablama prilikom donošenja odluka (ne znamo tačno koje karte protivnik ima u rukama, koje karte će doći u narednim rundama trgovina). Svako od rješenja moramo razmotriti sa stanovišta teorije velikih brojeva, koja kaže da će s dovoljno velikim uzorkom prosječna vrijednost slučajne varijable težiti njenoj očekivanoj vrijednosti.

Među posebnim formulama za izračunavanje očekivanja partnera, u pokeru je najprikladnije sljedeće:
Kada igrate poker mat. očekivanje se može izračunati i za opklade i za pozive. U prvom slučaju treba uzeti u obzir fold equity, a u drugom sopstvene šanse banke. Prilikom ocjenjivanja mat. očekivanja od određenog poteza, treba imati na umu da fold uvijek ima nula očekivanja. Stoga će odbacivanje karata uvijek biti isplativija odluka od bilo kojeg negativnog poteza.
Matematičko očekivanje (srednja populacija) je
Očekivanje vam govori šta možete očekivati (ili gubitak) za svaki rizik koji preuzmete. Kazina zarađuju novac novac, pošto je mat očekivanje od svih igara koje se u njima praktikuju, u korist kazina. Uz dovoljno dugu seriju igara, možete očekivati da će klijent izgubiti svoju novac, budući da su “šanse” u korist kazina. Međutim, profesionalni kazino špekulanti ograničavaju svoje igre na kratke periode, čime povećavaju šanse u svoju korist. Isto važi i za investiranje. Ako su vaša očekivanja pozitivna, možete zaraditi više novca tako što ćete napraviti mnogo trgovina u kratkom vremenu period vrijeme. Očekivanje je vaš procenat profita po pobjedi pomnožen vašim prosječnim profitom, minus vaša vjerovatnoća gubitka pomnožena vašim prosječnim gubitkom.

Poker se takođe može posmatrati sa stanovišta očekivanja mat. Možete pretpostaviti da je određeni potez isplativ, ali u nekim slučajevima možda neće biti najbolji jer je drugi potez isplativiji. Recimo da ste pogodili punu kuću u pokeru sa pet karata. Vaš protivnik se kladi. Znate da ako podignete opkladu, on će odgovoriti. Stoga se čini da je podizanje najbolje taktika. Ali ako podignete ulog, preostala dva špekulanta će definitivno odustati. Ali ako pozovete, imate puno povjerenje da će druga dva špekulanta nakon vas učiniti isto. Kada podignete svoju opkladu dobijate jednu jedinicu, a kada samo platite dobijate dve. Dakle, pozivanje vam daje veću pozitivnu očekivanu vrijednost i biće najbolja taktika.
Mat. Očekivanje takođe može dati ideju o tome koje poker taktike su manje isplative, a koje su isplativije. Na primjer, ako igrate određenu ruku i mislite da će vaš gubitak u prosjeku iznositi 75 centi uključujući ante, onda biste trebali odigrati tu ruku jer ovo je bolje nego odustati kada je ante $1.

Još jedan važan razlog za razumevanje suštine mate. očekivanje je da vam to daje osjećaj mira bez obzira da li ste dobili opkladu ili ne: ako ste dobro uložili ili odustali u pravo vrijeme, znat ćete da ste zaradili ili uštedjeli određenu svotu novca koju bi slabiji špekulant mogao ne sačuvaj. Mnogo je teže odustati ako ste uznemireni jer je vaš protivnik izvukao jaču ruku. Uz sve ovo, ono što ste uštedjeli tako što niste igrali, umjesto klađenja, dodaje se vašem dobitku po noći ili mjesečno.
Samo zapamtite da da ste promijenili ruke, protivnik bi vas pozvao, a kao što ćete vidjeti u članku o Fundamentalnoj teoremi pokera, ovo je samo jedna od vaših prednosti. Trebao bi biti sretan kada se ovo desi. Možda čak naučite da uživate u gubitku ruke jer znate da bi drugi špekulanti na vašoj poziciji izgubili mnogo više.

Kao što je spomenuto u primjeru igre s novčićima na početku, omjer profita po satu je međusobno povezan sa materijom očekivanja, a ovaj koncept je posebno važan za profesionalne špekulante. Kada idete da igrate poker, trebali biste mentalno procijeniti koliko možete osvojiti za sat vremena igre. U većini slučajeva morat ćete se osloniti na svoju intuiciju i iskustvo, ali možete koristiti i matematiku. Na primjer, igrate draw lowball i vidite da tri igrača klade $10, a zatim mijenjaju dvije karte, što je vrlo loša taktika, možete shvatiti da svaki put kada ulože $10 gube oko $2. Svaki od njih to radi osam puta na sat, što znači da sva trojica gube otprilike 48 dolara po satu. Vi ste jedan od preostala četiri špekulanta, koji su približno jednaki, tako da ova četiri špekulanta (i vi među njima) moraju podijeliti 48 dolara, svaki s profitom od 12 dolara po satu. Vaše kvote po satu u ovom slučaju su jednostavno jednake vašem udjelu u iznosu novca koji su izgubila tri loša špekulanta za sat vremena.
Matematičko očekivanje (srednja populacija) je
Tokom dugog vremenskog perioda, ukupan dobitak špekulanta je zbir njegovih matematičkih očekivanja u pojedinačnim rukama. Što više ruku igrate sa pozitivnim očekivanjima, više dobijate, i obrnuto, što više ruku igrate sa negativnim očekivanjima, više gubite. Kao rezultat toga, trebali biste odabrati igru koja može maksimizirati vaše pozitivno iščekivanje ili negirati vaše negativno iščekivanje tako da možete maksimizirati svoje dobitke po satu.

Pozitivna matematička očekivanja u strategiji igranja
Ako znate brojati karte, možete imati prednost u odnosu na kasino, sve dok vas ne primjete i izbace vas. Kazina vole pijane špekulante i ne podnose brojanje karata. Prednost će vam omogućiti da pobijedite više puta nego što izgubite tokom vremena. Dobro upravljanje novcem kada koristite kalkulacije očekivanih partnera može vam pomoći da izvučete više profita iz svoje prednosti i smanjite gubitke. Bez prednosti, bolje je dati novac u dobrotvorne svrhe. U igri na berzi prednost daje sistem igre koji stvara veći profit nego gubitak, razlika cijene i provizije. Nema upravljanje kapitalom neće spasiti loš sistem igranja.
Pozitivno očekivanje se definira kao vrijednost veća od nule. Što je ovaj broj veći, to je statističko očekivanje jače. Ako je vrijednost manja od nule, onda mat. očekivanje će također biti negativno. Što je veći modul negativne vrijednosti, to je situacija gora. Ako je rezultat nula, onda je čekanje rentabilno. Možete pobijediti samo kada imate pozitivna matematička očekivanja i razuman sistem igre. Igranje po intuiciji vodi do katastrofe.

Matematičko očekivanje i
Očekivanje mata je prilično tražen i popularan statistički pokazatelj kada se vrši berzansko trgovanje na finansijskim tržištima tržišta. Prije svega, ovaj parametar se koristi za analizu uspješnosti trgovina. Nije teško pretpostaviti da što je ova vrijednost veća, to je više razloga da se trgovina koja se proučava uspješnom smatra. Naravno, analiza rad trgovac se ne može napraviti samo koristeći ovaj parametar. Međutim, izračunata vrijednost u kombinaciji s drugim metodama procjene kvaliteta rad, može značajno poboljšati tačnost analize.

Očekivani mat se često računa u uslugama praćenja trgovačkih računa, što vam omogućava da brzo procijenite obavljeni posao na depozitu. Izuzeci uključuju strategije koje koriste neprofitabilne trgovine koje se ne koriste. Trader sreća ga može pratiti neko vrijeme, pa stoga možda neće biti nikakvih gubitaka u njegovom radu. U ovom slučaju neće se moći kretati samo prema matematičkom očekivanju, jer se rizici koji se koriste u radu neće uzeti u obzir.
U trgovanju dalje tržište mat se najčešće koristi kada se predviđa profitabilnost bilo koje strategije trgovanja ili kada se predviđa prihod trgovac na osnovu statističkih podataka iz njegovih prethodnih nadmetanje.
Matematičko očekivanje (srednja populacija) je
Što se tiče upravljanja novcem, veoma je važno shvatiti da ne postoji obrazac u trgovanju sa negativnim očekivanjima menadžment novac, koji svakako može donijeti visoku zaradu. Ako nastavite da igrate berza pod ovim uslovima, onda bez obzira na metodu menadžment novca, izgubit ćete cijeli račun, bez obzira koliko je bio na početku.
Ovaj aksiom važi ne samo za igre ili trgovine sa negativnim očekivanjima, već je istinit i za igre sa jednakim šansama. Stoga, jedini put kada imate šansu da zaradite na duge staze je ako izvršite trgovine sa pozitivnom očekivanom vrijednošću.

Razlika između negativnih i pozitivnih očekivanja je razlika između života i smrti. Nije važno koliko su očekivanja pozitivna ili negativna; Bitno je samo da li je pozitivno ili negativno. Stoga, prije razmatranja pitanja upravljanja kapital morate pronaći igru sa pozitivnim iščekivanjem.
Ako nemate tu igru, onda vas neće spasiti svo upravljanje novcem na svijetu. S druge strane, ako imate pozitivna očekivanja, možete ga, kroz pravilno upravljanje novcem, pretvoriti u funkciju eksponencijalnog rasta. Nije važno koliko su pozitivna očekivanja mala! Drugim riječima, nije važno koliko je profitabilan sistem trgovanja zasnovan na jednom ugovoru. Ako imate sistem koji osvaja $10 po ugovoru po trgovini (nakon provizija i proklizavanja), možete koristiti tehnike upravljanja kapital na način koji ga čini profitabilnijim od sistema koji pokazuje prosječan profit od 1.000 USD po trgovini (nakon provizija i proklizavanja).

Ono što je bitno nije koliko je sistem bio profitabilan, već koliko se sigurno može reći da će sistem pokazati barem minimalnu dobit u budućnosti. Stoga je najvažnija priprema koja se može izvršiti je osigurati da će sistem pokazati pozitivnu očekivanu vrijednost u budućnosti.
Da biste imali pozitivnu očekivanu vrijednost u budućnosti, veoma je važno da ne ograničavate stepene slobode vašeg sistema. Ovo se postiže ne samo eliminacijom ili smanjenjem broja parametara koji se optimizuju, već i smanjenjem što većeg broja sistemskih pravila. Svaki parametar koji dodate, svako pravilo koje napravite, svaka mala promjena koju napravite u sistemu smanjuje broj stupnjeva slobode. U idealnom slučaju, morate izgraditi prilično primitivan i jednostavan sistem koji će dosljedno generirati male profite na gotovo svakom tržištu. Opet, važno je da shvatite da nije važno koliko je sistem profitabilan, sve dok je profitabilan. Novac koji zaradite u trgovanju biće zarađen kroz efikasno upravljanje novcem.
Matematičko očekivanje (srednja populacija) je
Sistem trgovanja je jednostavno alat koji vam daje pozitivnu očekivanu vrijednost tako da možete koristiti upravljanje novcem. Sistemi koji rade (pokazuju barem minimalni profit) na samo jednom ili nekoliko tržišta, ili imaju različita pravila ili parametre za različita tržišta, najvjerovatnije neće dugo raditi u realnom vremenu. Problem kod većine tehnički orijentisanih trgovaca je što troše previše vremena i truda na optimizaciju različitih pravila i vrednosti parametara sistema trgovanja. Ovo daje potpuno suprotne rezultate. Umjesto da trošite energiju i kompjutersko vrijeme na povećanje profita trgovačkog sistema, svoju energiju usmjerite na povećanje nivoa pouzdanosti ostvarivanja minimalnog profita.
Znajući to upravljanje kapitalom je samo igra brojeva koja zahtijeva korištenje pozitivnih očekivanja, trgovac može prestati tražiti "sveti gral" trgovanja dionicama. Umjesto toga, može početi testirati svoju metodu trgovanja, saznati koliko je ova metoda logična i daje li pozitivna očekivanja. Pravilne metode upravljanja novcem, primijenjene na bilo koju, čak i vrlo osrednju metodu trgovanja, sami će obaviti ostatak posla.

Da bi svaki trgovac uspio u svom poslu, potrebno je riješiti tri najvažnija zadatka:. Da bi se osiguralo da broj uspješnih transakcija premašuje neizbježne greške i pogrešne proračune; Postavite svoj sistem trgovanja tako da imate priliku da zarađujete novac što je češće moguće; Ostvarite stabilne pozitivne rezultate iz svog poslovanja.
I ovdje, nama zaposlenim trgovcima, mate može biti dobra pomoć. očekivanje. Ovaj termin je jedan od ključnih u teoriji vjerovatnoće. Uz njegovu pomoć možete dati prosječnu procjenu neke slučajne vrijednosti. Očekivanje slučajne varijable slično je centru gravitacije, ako zamislite sve moguće vjerovatnoće kao tačke sa različitim masama.

U odnosu na strategiju trgovanja, očekivanje dobiti (ili gubitka) najčešće se koristi za procenu njene efikasnosti. Ovaj parametar se definiše kao zbir proizvoda datih nivoa dobiti i gubitka i verovatnoće njihovog nastanka. Na primjer, razvijena strategija trgovanja pretpostavlja da će 37% svih operacija donijeti profit, a preostali dio - 63% - biti neprofitabilan. Istovremeno, prosjek prihod od uspješne trgovine će biti 7 dolara, a prosječan gubitak će biti 1,4 dolara. Izračunajmo matematiku. očekivanja trgovanja korišćenjem ovog sistema:
Šta znači ovaj broj? Kaže da ćemo, slijedeći pravila ovog sistema, u prosjeku dobiti 1.708 dolara od svake zatvorene transakcije. Pošto je rezultujuća ocena efikasnosti veća od nule, takav sistem se može koristiti za pravi rad. Ako se, kao rezultat izračunavanja mat, očekivanje pokaže negativnim, onda to već ukazuje na prosječan gubitak i to će dovesti do propasti.
Veličina dobiti po transakciji se takođe može izraziti kao relativna vrijednost u obliku %. Na primjer:
Procenat prihoda po 1 transakciji je 5%;
Procenat uspešnog trgovanja je 62%;
Procenat gubitka po 1 trgovini - 3%;
Procenat neuspešnih transakcija je 38%;
U ovom slučaju, mat. očekivanje će biti:
Odnosno, prosječna trgovina će donijeti 1,96%.
Moguće je razviti sistem koji će, uprkos dominaciji neprofitabilnih trgovina, dati pozitivan rezultat, budući da je MO>0.
Međutim, samo čekanje nije dovoljno. Teško je zaraditi novac ako sistem daje vrlo malo trgovačkih signala. U ovom slučaju, to će biti uporedivo sa bankarskom kamatom. Neka svaka operacija proizvodi u prosjeku samo 0,5 dolara, ali šta ako sistem uključuje 1000 operacija godišnje? To će biti veoma značajan iznos u relativno kratkom vremenu. Iz ovoga logično proizilazi da se još jednom posebnom karakteristikom dobrog trgovačkog sistema može smatrati kratak period držanja pozicija.

Izvori i linkovi
dic.academic.ru - akademski online rječnik
mathematics.ru - obrazovna web stranica iz matematike
nsu.ru - obrazovna web stranica Novosibirskog državnog univerziteta
webmath.ru je obrazovni portal za studente, kandidate i školarce.
exponenta.ru obrazovna matematička web stranica
ru.tradimo.com - besplatna škola online trgovanja
crypto.hut2.ru - multidisciplinarni informativni resurs
poker-wiki.ru - besplatna enciklopedija pokera
sernam.ru - Naučna biblioteka izabranih publikacija prirodnih nauka
reshim.su - web stranica MI ĆEMO RJEŠITI probleme sa testom
unfx.ru - Forex na UNFX: obuka, trgovački signali, upravljanje povjerenjem
- — matematičko očekivanje Jedna od numeričkih karakteristika slučajne varijable, koja se često naziva njenim teorijskim prosjekom. Za diskretnu slučajnu varijablu X matematički ... ... Vodič za tehnički prevodilacOČEKIVANA VRIJEDNOST- (očekivana vrijednost) Prosječna vrijednost distribucije ekonomske varijable koju može uzeti. Ako je rt cijena proizvoda u trenutku t, njegovo matematičko očekivanje se označava sa Ept. Da naznači trenutak u vremenu do kojeg ... ... Ekonomski rječnik
Očekivana vrijednost- prosječna vrijednost slučajne varijable. Matematičko očekivanje je deterministička veličina. Aritmetička sredina realizacija slučajne varijable je procjena matematičkog očekivanja. Prosjek… … Službena terminologija - (prosječna vrijednost) slučajne varijable - numerička karakteristika slučajne varijable. Ako je slučajna varijabla definirana na prostoru vjerovatnoće (pogledajte Teoriju vjerovatnoće), tada njen M. o. MX (ili EX) je definiran kao Lebesgueov integral: gdje je... Fizička enciklopedija
OČEKIVANA VRIJEDNOST- slučajna varijabla je njena numerička karakteristika. Ako slučajna varijabla X ima funkciju distribucije F(x), tada njen M. o. će: . Ako je distribucija X diskretna, onda M.o.: , gdje je x1, x2, ... moguće vrijednosti diskretne slučajne varijable X; p1... Geološka enciklopedija
OČEKIVANA VRIJEDNOST- Engleski očekivanu vrijednost njemački Erwartung mathematische. Stohastička sredina ili centar disperzije slučajne varijable. Antinazi. Enciklopedija sociologije, 2009 ... Enciklopedija sociologije
Očekivana vrijednost- Vidi takođe: Uslovno matematičko očekivanje Matematičko očekivanje je prosečna vrednost slučajne varijable, distribucija verovatnoće slučajne varijable, razmatra se u teoriji verovatnoće. U literaturi na engleskom jeziku iu matematičkoj... ... Wikipediji
Očekivana vrijednost- 1.14 Matematičko očekivanje E (X) gdje je xi vrijednost diskretne slučajne varijable; p = P (X = xi); f(x) gustina kontinuirane slučajne varijable * Ako ovaj izraz postoji u smislu apsolutne konvergencije Izvor... Rječnik-priručnik pojmova normativne i tehničke dokumentacije
Knjige
Koristimo kolačiće za najbolju prezentaciju naše stranice. Nastavljajući koristiti ovu stranicu, slažete se s ovim. uredu
Matematičko očekivanje proizvoda dvije slučajne varijable jednako je proizvodu njihovih matematičkih očekivanja plus korelacijski moment:
Dokaz. Poći ćemo od definicije korelacionog momenta:
Transformirajmo ovaj izraz koristeći svojstva matematičkog očekivanja:
što je očigledno ekvivalentno formuli (10.2.17).
Ako slučajne varijable nisu u korelaciji, onda formula (10.2.17) poprima oblik:
to jest, matematičko očekivanje proizvoda dvije nekorelirane slučajne varijable jednako je proizvodu njihovih matematičkih očekivanja.
Ova pozicija je poznata kao teorema množenja matematičkih očekivanja.
Formula (10.2.17) nije ništa drugo do izraz drugog mešovitog centralnog momenta sistema kroz drugi mešoviti početni trenutak i matematička očekivanja:
![]() . (10.2.19)
. (10.2.19)
Ovaj izraz se često koristi u praksi kada se izračunava korelacioni moment na isti način na koji se za jednu slučajnu varijablu varijansa često izračunava kroz drugi početni trenutak i matematičko očekivanje.
Teorema množenja matematičkih očekivanja generalizirana je na proizvoljan broj faktora, samo u ovom slučaju za njenu primjenu nije dovoljno da su veličine nekorelirane, već je potrebno da se pojave neki viši mješoviti momenti čiji broj zavisi na broj pojmova u proizvodu, nestaju. Ovi uslovi su svakako zadovoljeni ako su slučajne varijable uključene u proizvod nezavisne. U ovom slučaju
 , (10.2.20)
, (10.2.20)
to jest, matematičko očekivanje proizvoda nezavisnih slučajnih varijabli jednako je proizvodu njihovih matematičkih očekivanja.
Ovaj prijedlog se može lako dokazati potpunom indukcijom.
Varijanca proizvoda nezavisnih slučajnih varijabli
Dokažimo to za nezavisne veličine
Dokaz. Označimo . Po definiciji varijanse
Pošto su količine nezavisne, i
Kada su nezavisne, količine su takođe nezavisne; dakle,
, ![]()
Ali ne postoji ništa više od drugog početnog momenta veličine, i stoga se izražava kroz disperziju:
![]() ;
;
slično
![]() .
.
Zamjenom ovih izraza u formulu (10.2.22) i dovođenjem sličnih pojmova dolazimo do formule (10.2.21).
U slučaju kada se centrirane slučajne varijable (varijable sa matematičkim očekivanjima jednakim nuli) pomnože, formula (10.2.21) ima oblik:
![]() , (10.2.23)
, (10.2.23)
odnosno varijansa proizvoda nezavisnih centriranih slučajnih varijabli jednaka je proizvodu njihovih varijansi.
Najveći momenti zbira slučajnih varijabli
U nekim slučajevima potrebno je izračunati najveće momente zbira nezavisnih slučajnih varijabli. Dokažimo neke povezane relacije.
1) Ako su veličine nezavisne, onda
Matematičko očekivanje (prosječna vrijednost) slučajne varijable X dato na diskretnom prostoru vjerovatnoće je broj m =M[X]=∑x i p i ako se niz apsolutno konvergira.
Svrha usluge. Korištenje online usluge izračunata su matematička očekivanja, varijansa i standardna devijacija(vidi primjer). Dodatno, iscrtan je graf funkcije distribucije F(X).
Svojstva matematičkog očekivanja slučajne varijable
- Matematičko očekivanje konstantne vrijednosti jednako je samoj sebi: M[C]=C, C – konstanta;
- M=C M[X]
- Matematičko očekivanje zbira slučajnih varijabli jednako je zbiru njihovih matematičkih očekivanja: M=M[X]+M[Y]
- Matematičko očekivanje proizvoda nezavisnih slučajnih varijabli jednako je proizvodu njihovih matematičkih očekivanja: M=M[X] M[Y] , ako su X i Y nezavisni.
Svojstva disperzije
- Varijanca konstantne vrijednosti je nula: D(c)=0.
- Konstantni faktor se može izvaditi ispod znaka disperzije kvadriranjem: D(k*X)= k 2 D(X).
- Ako su slučajne varijable X i Y nezavisne, tada je varijansa sume jednaka zbroju varijansi: D(X+Y)=D(X)+D(Y).
- Ako su slučajne varijable X i Y zavisne: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- Sljedeća računska formula vrijedi za disperziju:
D(X)=M(X 2)-(M(X)) 2
Primjer. Poznata su matematička očekivanja i varijanse dvije nezavisne slučajne varijable X i Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Naći matematičko očekivanje i varijansu slučajne varijable Z=9X-8Y+7.
Rješenje. Na osnovu svojstava matematičkog očekivanja: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Na osnovu svojstava disperzije: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algoritam za izračunavanje matematičkog očekivanja
Svojstva diskretnih slučajnih varijabli: sve njihove vrijednosti mogu se prenumerisati prirodnim brojevima; Dodijelite svakoj vrijednosti vjerovatnoću različitu od nule.- Parove množimo jedan po jedan: x i sa p i .
- Dodajte proizvod svakog para x i p i .
Na primjer, za n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Primjer br. 1.
| x i | 1 | 3 | 4 | 7 | 9 |
| p i | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Matematičko očekivanje pronalazimo pomoću formule m = ∑x i p i .
Očekivanje M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Pronalažemo varijansu koristeći formulu d = ∑x 2 i p i - M[x] 2 .
Varijanca D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Standardna devijacija σ(x).
σ = sqrt(D[X]) = sqrt(7,69) = 2,78
Primjer br. 2. Diskretna slučajna varijabla ima sljedeću seriju distribucije:
| X | -10 | -5 | 0 | 5 | 10 |
| R | A | 0,32 | 2a | 0,41 | 0,03 |
Rješenje. Vrijednost a se nalazi iz relacije: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0,76 + 3 a = 1 ili 0,24=3 a , odakle je a = 0,08
Primjer br. 3. Odrediti zakon raspodjele diskretne slučajne varijable ako je poznata njena varijansa i x 1
p 1 =0,3; p 2 =0,3; p 3 =0,1; p 4 =0,3
d(x)=12,96
Rješenje.
Ovdje trebate kreirati formulu za pronalaženje varijanse d(x):
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
gdje je očekivanje m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Za naše podatke
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
ili -9/100 (x 2 -20x+96)=0
U skladu s tim, moramo pronaći korijene jednadžbe, a bit će ih dva.
x 3 =8, x 3 =12
Odaberite onaj koji zadovoljava uslov x 1
Zakon distribucije diskretne slučajne varijable
x 1 =6; x 2 =9; x 3 =12; x 4 =15
p 1 =0,3; p 2 =0,3; p 3 =0,1; p 4 =0,3
Kao što je već poznato, zakon raspodjele u potpunosti karakterizira slučajnu varijablu. Međutim, često je zakon distribucije nepoznat i čovjek se mora ograničiti na manje informacija. Ponekad je čak isplativije koristiti brojeve koji ukupno opisuju slučajnu varijablu; takvi brojevi se nazivaju numeričke karakteristike slučajne varijable.
Jedna od važnih numeričkih karakteristika je matematičko očekivanje.
Matematičko očekivanje je približno jednako prosječnoj vrijednosti slučajne varijable.
Matematičko očekivanje diskretne slučajne varijable je zbir proizvoda svih njegovih mogućih vrijednosti i njihovih vjerovatnoća.
Ako je slučajna varijabla karakterizirana konačnim nizom distribucije:
| X | x 1 | x 2 | x 3 | … | x n |
| R | p 1 | p 2 | p 3 | … | r p |
zatim matematičko očekivanje M(X) određena formulom:
Matematičko očekivanje kontinuirane slučajne varijable određeno je jednakošću:
gdje je gustina vjerovatnoće slučajne varijable X.
Primjer 4.7. Pronađite matematičko očekivanje broja poena koji se pojavljuju prilikom bacanja kocke.
Rješenje:
Slučajna vrijednost X uzima vrijednosti 1, 2, 3, 4, 5, 6. Kreirajmo zakon njegove distribucije:
| X | ||||||
| R |
Tada je matematičko očekivanje:
Svojstva matematičkog očekivanja:
1. Matematičko očekivanje konstantne vrijednosti jednako je samoj konstanti:
M (S) = S.
2. Konstantni faktor se može izvaditi iz predznaka matematičkog očekivanja:
M (CX) = CM (X).
3. Matematičko očekivanje proizvoda dvije nezavisne slučajne varijable jednako je proizvodu njihovih matematičkih očekivanja:
M(XY) = M(X)M(Y).
Primjer 4.8. Nezavisne slučajne varijable X I Y dati su sljedećim zakonima o distribuciji:
| X | Y | ||||||
| R | 0,6 | 0,1 | 0,3 | R | 0,8 | 0,2 |
Pronađite matematičko očekivanje slučajne varijable XY.
Rješenje.
Nađimo matematička očekivanja svake od ovih veličina:
Slučajne varijable X I Y nezavisno, stoga je traženo matematičko očekivanje:
M(XY) = M(X)M(Y)=
Posljedica. Matematičko očekivanje proizvoda nekoliko međusobno nezavisnih slučajnih varijabli jednako je proizvodu njihovih matematičkih očekivanja.
4. Matematičko očekivanje zbira dvije slučajne varijable jednako je zbiru matematičkih očekivanja pojmova:
M (X + Y) = M (X) + M (Y).
Posljedica. Matematičko očekivanje sume nekoliko slučajnih varijabli jednako je zbiru matematičkih očekivanja termina.
Primjer 4.9. Ispaljuju se 3 hica sa vjerovatnoćom pogađanja mete jednakim p 1 = 0,4; p2= 0,3 i p 3= 0,6. Pronađite matematičko očekivanje ukupnog broja pogodaka.
Rješenje.
Broj pogodaka na prvom mecu je nasumična varijabla X 1, koji može uzeti samo dvije vrijednosti: 1 (pogodan) sa vjerovatnoćom p 1= 0,4 i 0 (promašaj) sa vjerovatnoćom q 1 = 1 – 0,4 = 0,6.
Matematičko očekivanje broja pogodaka pri prvom metku jednako je vjerovatnoći pogotka:
Slično, nalazimo matematička očekivanja broja pogodaka za drugi i treći hitac:
M(X 2)= 0,3 i M(X 3)= 0,6.
Ukupan broj pogodaka je također slučajna varijabla koja se sastoji od zbira pogodaka u svakom od tri hica:
X = X 1 + X 2 + X 3.
Potrebna matematička očekivanja X nalazimo teoremom o matematičkom očekivanju sume:
M(X) = M(X l + X 2 + X 3) = M(X 1) + M(X 2) + M (X 3)= 0,4 + 0,3 + 0,6 = 1,3 (pogoci).
– broj dječaka među 10 novorođenčadi.
Apsolutno je jasno da se taj broj ne zna unaprijed, a sljedećih deset rođenih djece može uključivati:
Ili momci - jedan i jedini od navedenih opcija.
I, kako biste ostali u formi, malo fizičkog vaspitanja:
– daljina skoka u dalj (u nekim jedinicama).
Ni majstor sporta to ne može predvidjeti :)
Međutim, vaše hipoteze?
2) Kontinuirana slučajna varijabla – prihvata Sve numeričke vrijednosti iz nekog konačnog ili beskonačnog intervala.
Bilješka : u obrazovnoj literaturi popularne su skraćenice DSV i NSV
Prvo, analizirajmo diskretnu slučajnu varijablu, a zatim - kontinuirano.
Zakon distribucije diskretne slučajne varijable
- Ovo dopisivanje između mogućih vrijednosti ove veličine i njihovih vjerovatnoća. Zakon je najčešće zapisan u tabeli: 
Termin se često pojavljuje red
distribucija, ali u nekim situacijama zvuči dvosmisleno, pa ću se držati "zakona".
I sada veoma važna tačka: od slučajne varijable Nužnoće prihvatiti jedna od vrednosti, zatim se formiraju odgovarajući događaji puna grupa a zbir vjerovatnoća njihovog pojavljivanja jednak je jedan:
ili, ako je napisano sažeto:
Tako, na primjer, zakon raspodjele vjerovatnoće bodova bačenih na kockicu ima sljedeći oblik: 
Bez komentara.
Možda ste pod utiskom da diskretna slučajna varijabla može poprimiti samo “dobre” vrijednosti cijelih brojeva. Razbijmo iluziju - mogu biti bilo šta:
Primjer 1
Neka igra ima sljedeći pobjednički zakon distribucije: 
...o takvim zadacima vjerovatno ste dugo sanjali :) Odaću vam tajnu - i ja. Pogotovo nakon završetka radova teorija polja.
Rješenje: budući da slučajna varijabla može uzeti samo jednu od tri vrijednosti, formiraju se odgovarajući događaji puna grupa, što znači da je zbir njihovih vjerovatnoća jednak jedan: ![]()
Razotkrivanje "partizana": ![]()
– dakle, vjerovatnoća osvajanja konvencionalnih jedinica je 0,4.
Kontrola: to je ono u šta smo trebali da se uverimo.
Odgovori:
Nije neuobičajeno kada trebate sami sastaviti zakon o raspodjeli. Za to koriste klasična definicija vjerovatnoće, teoreme množenja/sabiranja za vjerovatnoće događaja i drugi čips tervera:
Primjer 2
Kutija sadrži 50 lutrijskih listića, među kojima je 12 dobitnih, a 2 od njih osvajaju po 1000 rubalja, a ostale - po 100 rubalja. Sastavite zakon za raspodjelu slučajne varijable - veličine dobitka, ako se iz kutije nasumično izvuče jedan listić.
Rješenje: kao što ste primijetili, vrijednosti slučajne varijable se obično stavljaju u u rastućem redosledu. Stoga počinjemo s najmanjim dobicima, odnosno rubalja.
Ukupno ima 50 takvih karata - 12 = 38, a prema klasična definicija:
– vjerovatnoća da će nasumično izvučena karta biti gubitnik.
U ostalim slučajevima sve je jednostavno. Vjerovatnoća osvajanja rublja je:
Provjerite: – a ovo je posebno prijatan trenutak takvih zadataka!
Odgovori: željeni zakon raspodjele dobitaka: ![]()
Sljedeći zadatak morate riješiti sami:
Primjer 3
Vjerovatnoća da će strijelac pogoditi metu je . Nacrtajte zakon raspodjele za slučajnu varijablu - broj pogodaka nakon 2 hica.
...znala sam da ti nedostaje :) Da se prisjetimo teoreme množenja i sabiranja. Rješenje i odgovor nalaze se na kraju lekcije.
Zakon distribucije u potpunosti opisuje slučajnu varijablu, ali u praksi može biti korisno (a ponekad i korisnije) znati samo dio nje numeričke karakteristike .
Očekivanje diskretne slučajne varijable
Jednostavno rečeno, ovo je prosječna očekivana vrijednost kada se testiranje ponavlja mnogo puta. Neka slučajna varijabla uzima vrijednosti s vjerovatnoćom ![]() respektivno. Tada je matematičko očekivanje ove slučajne varijable jednako zbroj proizvoda sve njegove vrijednosti na odgovarajuće vjerovatnoće:
respektivno. Tada je matematičko očekivanje ove slučajne varijable jednako zbroj proizvoda sve njegove vrijednosti na odgovarajuće vjerovatnoće:
ili srušeno: ![]()
Izračunajmo, na primjer, matematičko očekivanje slučajne varijable - broj bodova bačenih na kockicu:
Sada se prisjetimo naše hipotetičke igre: 
Postavlja se pitanje da li je uopšte isplativo igrati ovu igru? ...ko ima utisaka? Dakle, ne možete to da kažete „na ruku“! Ali na ovo pitanje se lako može odgovoriti izračunavanjem matematičkog očekivanja, u suštini - prosjećna težina po vjerovatnoći pobjede:
Dakle, matematičko očekivanje ove igre gubljenje.
Ne vjerujte svojim utiscima - vjerujte brojevima!
Da, ovdje možete pobijediti 10 ili čak 20-30 puta uzastopno, ali na duge staze čeka nas neizbježna propast. I ne bih ti savjetovao da igraš takve igrice :) Pa, možda samo za zabavu.
Iz svega navedenog proizilazi da matematičko očekivanje više nije RANDOM vrijednost.
Kreativni zadatak za samostalno istraživanje:
Primjer 4
G. X igra evropski rulet koristeći sledeći sistem: on stalno kladi 100 rubalja na „crveno“. Nacrtajte zakon raspodjele slučajne varijable - njenog dobitka. Izračunajte matematičko očekivanje dobitaka i zaokružite ga na najbližu kopejku. Koliko prosjek Da li igrač gubi za svakih sto u koje je uložio?
Referenca : Evropski rulet sadrži 18 crvenih, 18 crnih i 1 zeleni sektor (“nula”). Ako se pojavi „crveno“, igraču se plaća dupla opklada, u suprotnom ide u prihod kasina
Postoje mnogi drugi sistemi ruleta za koje možete kreirati sopstvene tabele verovatnoće. Ali to je slučaj kada nam nisu potrebni nikakvi zakoni distribucije ili tabele, jer je sigurno utvrđeno da će matematička očekivanja igrača biti potpuno ista. Jedina stvar koja se mijenja od sistema do sistema je