Grafičko rješenje kvadratne jednadžbe Ojačati sposobnost građenja grafova različitih funkcija; Razvijati sposobnost grafičkog rješavanja kvadratnih jednadžbi. Prezentacija iz matematike na temu "rješavanje zadataka pomoću grafova funkcija"

Grafičko rješenje jednačina

Heyday, 2009

Uvod

Potreba za rješavanjem kvadratnih jednačina u antičko doba bila je uzrokovana potrebom rješavanja problema vezanih za pronalaženje površina zemljišta i sa vojnim iskopavanjima, kao i sa razvojem same astronomije i matematike. Babilonci su bili u stanju da reše kvadratne jednačine oko 2000. godine pre nove ere. Pravilo za rješavanje ovih jednačina, postavljeno u babilonskim tekstovima, u suštini se poklapa sa modernim, ali nije poznato kako su Babilonci došli do ovog pravila.

Formule za rješavanje kvadratnih jednačina u Evropi su prvi put izložene u Knjizi Abacus, koju je 1202. godine napisao italijanski matematičar Leonardo Fibonacci. Njegova knjiga je doprinijela širenju algebarskog znanja ne samo u Italiji, već iu Njemačkoj, Francuskoj i drugim evropskim zemljama.

Ali opšte pravilo za rešavanje kvadratnih jednačina, sa svim mogućim kombinacijama koeficijenata b i c, formulisao je u Evropi tek 1544. godine M. Stiefel.

Godine 1591 Francois Viet uvedene formule za rješavanje kvadratnih jednadžbi.

U starom Babilonu su mogli riješiti neke vrste kvadratnih jednačina.

Diofant Aleksandrijski I Euclid, Al-Khwarizmi I Omar Khayyam rješavanje jednadžbi geometrijskim i grafičkim metodama.

U 7. razredu smo učili funkcije y = C, y =kx, y =kx+ m, y =x 2,y = –x 2, u 8. razredu - y = √x, y =|x|, y =sjekira2 + bx+ c, y =k/ x. U udžbeniku algebre za 9. razred vidio sam funkcije koje mi još nisu bile poznate: y =x 3, y =x 4,y =x 2n, y =x- 2n, y = 3√x, (x– a) 2 + (y –b) 2 = r 2 i drugi. Postoje pravila za konstruisanje grafova ovih funkcija. Pitao sam se da li postoje druge funkcije koje poštuju ova pravila.

Moj posao je proučavanje grafova funkcija i grafički rješavanje jednadžbi.

1. Koje su funkcije?

Graf funkcije je skup svih točaka koordinatne ravnine, čije su apscise jednake vrijednostima argumenata, a ordinate jednake odgovarajućim vrijednostima funkcije.

Linearna funkcija je data jednadžbom y =kx+ b, Gdje k I b- neki brojevi. Grafikon ove funkcije je prava linija.

Inverzna proporcionalna funkcija y =k/ x, gdje je k ¹ 0. Graf ove funkcije naziva se hiperbola.

Funkcija (x– a) 2 + (y –b) 2 = r2 , Gdje A, b I r- neki brojevi. Graf ove funkcije je kružnica polumjera r sa centrom u tački A ( A, b).

Kvadratna funkcija y= sjekira2 + bx+ c Gdje A,b, With– neki brojevi i A¹ 0. Grafikon ove funkcije je parabola.

Jednačina at2 (a– x) = x2 (a+ x) . Grafikon ove jednačine će biti kriva koja se zove strofoid.

/>Equation (x2 + y2 ) 2 = a(x2 – y2 ) . Graf ove jednačine naziva se Bernulijeva lemniskata.

Jednačina. Graf ove jednadžbe naziva se astroid.

Curve (x2 y2 – 2 sjekire)2 =4 a2 (x2 + y2 ) . Ova kriva se naziva kardioida.

Funkcije: y =x 3 – kubna parabola, y =x 4, y = 1/x 2.

2. Pojam jednadžbe i njeno grafičko rješenje

Jednačina– izraz koji sadrži varijablu.

Riješite jednačinu- to znači pronaći sve njegove korijene, ili dokazati da oni ne postoje.

Korijen jednadžbe je broj koji, kada se zameni u jednačinu, daje tačnu numeričku jednakost.

Grafičko rješavanje jednačina omogućava vam da pronađete tačnu ili približnu vrijednost korijena, omogućava vam da pronađete broj korijena jednadžbe.

Prilikom konstruiranja grafova i rješavanja jednadžbi koriste se svojstva funkcije, zbog čega se metoda često naziva funkcionalno-grafičkom.

Da bismo riješili jednačinu, "podijelimo" je na dva dijela, uvedemo dvije funkcije, izgradimo njihove grafove i pronađemo koordinate tačaka presjeka grafova. Apscise ovih tačaka su korijeni jednadžbe.

3. Algoritam za crtanje grafa funkcije

Poznavanje grafa funkcije y =f(x) , možete graditi grafove funkcija y =f(x+ m) ,y =f(x)+ l I y =f(x+ m)+ l. Svi ovi grafovi se dobijaju iz grafa funkcije y =f(x) koristeći paralelnu transformaciju prijenosa: to │ m│ jedinice skale desno ili lijevo duž x-ose i dalje │ l│ jedinice razmjera gore ili dolje duž ose y.

4. Grafičko rješenje kvadratne jednadžbe

Koristeći kvadratnu funkciju kao primjer, razmotrit ćemo grafičko rješenje kvadratne jednadžbe. Graf kvadratne funkcije je parabola.

Šta su stari Grci znali o paraboli?

Savremeni matematički simbolizam nastao je u 16. veku.

Drevni grčki matematičari nisu imali ni koordinatnu metodu ni koncept funkcije. Ipak, oni su detaljno proučavali svojstva parabole. Genijalnost drevnih matematičara je jednostavno nevjerojatna - na kraju krajeva, mogli su koristiti samo crteže i verbalne opise zavisnosti.

Najpotpunije je istražio parabolu, hiperbolu i elipsu Apolonije iz Perge, koji je živio u 3. vijeku prije nove ere. On je tim krivuljama dao imena i naznačio koje uslove ispunjavaju tačke koje leže na ovoj ili onoj krivulji (na kraju krajeva, nije bilo formula!).

Postoji algoritam za konstruisanje parabole:

Pronađite koordinate vrha parabole A (x0; y0): X=- b/2 a;

y0=axo2+in0+s;

Naći os simetrije parabole (prava x=x0);

PAGE_BREAK--

Sastavljamo tablicu vrijednosti za izgradnju kontrolnih tačaka;

Konstruišemo rezultirajuće tačke i konstruišemo tačke koje su im simetrične u odnosu na os simetrije.

1. Koristeći algoritam, konstruisaćemo parabolu y= x2 – 2 x– 3 . Apscise tačaka preseka sa osom x i postoje korijeni kvadratne jednadžbe x2 – 2 x– 3 = 0.

Postoji pet načina da se ova jednačina riješi grafički.

2. Podijelimo jednačinu na dvije funkcije: y= x2 I y= 2 x+ 3

3. Podijelimo jednačinu na dvije funkcije: y= x2 –3 I y=2 x. Korijeni jednadžbe su apscise tačaka presjeka parabole i prave.

4. Transformirajte jednačinu x2 – 2 x– 3 = 0 izolacijom kompletnog kvadrata u funkcije: y= (x–1) 2 I y=4. Korijeni jednadžbe su apscise tačaka presjeka parabole i prave.

5. Podijelite obje strane člana jednačine po članu x2 – 2 x– 3 = 0 on x, dobijamo x– 2 – 3/ x= 0 , podijelimo ovu jednačinu na dvije funkcije: y= x– 2, y= 3/ x. Korijeni jednadžbe su apscise tačaka presjeka prave i hiperbole.

5. Grafičko rješenje stepenskih jednačinan

Primjer 1. Riješite jednačinu x5 = 3 – 2 x.

y= x5 , y= 3 – 2 x.

odgovor: x = 1.

Primjer 2. Riješite jednačinu 3 √ x= 10 – x.

Korijeni ove jednadžbe su apscisa točke presjeka grafova dvije funkcije: y= 3 √ x, y= 10 – x.

odgovor: x = 8.

Zaključak

Nakon što smo pogledali grafikone funkcija: y =sjekira2 + bx+ c, y =k/ x, u = √x, y =|x|, y =x 3, y =x 4,y = 3√x, Primijetio sam da su svi ovi grafovi građeni po pravilu paralelnog prevođenja u odnosu na osi x I y.

Na primjeru rješavanja kvadratne jednačine možemo zaključiti da je grafička metoda primjenjiva i za jednačine stepena n.

Grafičke metode za rješavanje jednačina su lijepe i razumljive, ali ne daju 100% garanciju rješavanja bilo koje jednačine. Apscise presječnih tačaka grafova mogu biti približne.

U 9. razredu i srednjoj školi nastaviću da se upoznajem sa ostalim funkcijama. Zanima me da li se te funkcije pridržavaju pravila paralelnog prijenosa prilikom konstruiranja svojih grafova.

Iduće godine bih takođe želeo da razmotrim pitanja grafičkog rešavanja sistema jednačina i nejednačina.

Književnost

1. Algebra. 7. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

2. Algebra. 8. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

3. Algebra. 9. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

4. Glazer G.I. Istorija matematike u školi. VII–VIII razredi. – M.: Obrazovanje, 1982.

5. Časopis Matematika br. 5 2009; br. 8 2007; br. 23 2008.

6. Web stranice za grafičko rješenje jednačina na Internetu: Tol VIKI; stimul.biz/ru; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Grafičko rješenje jednačina

Heyday, 2009

- UVOD -

Ali opšte pravilo za rešavanje kvadratnih jednačina, sa svim mogućim kombinacijama koeficijenata b i c, formulisao je u Evropi tek 1544. godine M. Stiefel.

Godine 1591 Francois Viet uvedene formule za rješavanje kvadratnih jednadžbi.

U starom Babilonu su mogli riješiti neke vrste kvadratnih jednačina.

Diofant Aleksandrijski I Euclid, Al-Khwarizmi I Omar Khayyam rješavanje jednadžbi geometrijskim i grafičkim metodama.

U 7. razredu smo učili funkcije y = C, y =kx, y = kx+ m, y =x 2 ,y =- x 2 , u 8. razredu - y = vx, y =|x|, at = sjekira 2 + bx+ c, y =k / x. U udžbeniku algebre za 9. razred vidio sam funkcije koje mi još nisu bile poznate: y =x 3 , at = x 4 ,y =x 2n, at = x - 2n, at = 3v x, (x - a) 2 + (y -b) 2 = r 2 i drugi. Postoje pravila za konstruisanje grafova ovih funkcija. Pitao sam se da li postoje druge funkcije koje poštuju ova pravila.

Moj posao je proučavanje grafova funkcija i grafički rješavanje jednadžbi.

1. Koje su funkcije?

Graf funkcije je skup svih točaka koordinatne ravnine, čije su apscise jednake vrijednostima argumenata, a ordinate jednake odgovarajućim vrijednostima funkcije.

Linearna funkcija je data jednadžbom y =kx + b, Gdje k I b- neki brojevi. Grafikon ove funkcije je prava linija.

Inverzna proporcionalna funkcija y =k/ x, gdje je k 0. Graf ove funkcije naziva se gyrbola.

Funkcija (x - a) 2 + (y -b) 2 = r 2 , Gdje A, b I r- neki brojevi. Graf ove funkcije je kružnica polumjera r sa centrom u tački A ( A, b).

Kvadratna funkcija y = sjekira 2 + bx + c Gdje A,b, With- neki brojevi i A 0. Grafikon ove funkcije je parabola.

Jednačina at 2 (a - x) = x 2 (a+ x) . Grafikon ove jednačine će biti kriva koja se zove strofoid.

Jednačina (x 2 + y 2 ) 2 = a (x 2 - y 2 ) . Grafikon ove jednačine naziva se Bernulijeva Lemka.

Jednačina. Graf ove jednadžbe naziva se astroid.

Curve (x 2 y 2 - 2 sjekira) 2 =4 a 2 (x 2 + y 2 ) . Ova kriva se naziva kardioida.

Funkcije: y =x 3 - kubična parabola, y =x 4 , y = 1/x 2 .

2. Pojam jednadžbe i njeno grafičko rješenje

Jednačina- izraz koji sadrži vreme.

Riješite jednačinu- to znači pronaći sve njegove korijene, ili dokazati da oni ne postoje.

Korijen jednadžbe- ovo je broj koji, kada se zameni u jednačinu, daje tačnu numeričku jednakost.

Grafičko rješavanje jednačina omogućava vam da pronađete tačnu ili približnu vrijednost korijena, omogućava vam da pronađete broj korijena jednadžbe.

Prilikom konstruiranja grafova i rješavanja jednadžbi koriste se svojstva funkcije, pa se metoda često naziva funkcionalno-grafičkom.

Da bismo riješili jednačinu, "podijelimo" je na dva dijela, uvedemo dvije funkcije, konstruiramo njihove grafove i pronađemo koordinate presječnih tačaka grafova. Apscise ovih tačaka su korijeni jednadžbe.

3. Algoritam za crtanje funkcije

Poznavanje grafa funkcije y =f(x) , možete graditi grafove funkcija y =f (x+ m) ,y =f(x)+ l I y =f (x+ m)+ l. Svi ovi grafovi se dobijaju iz grafa funkcije y =f(x) koristeći paralelnu transformaciju: to ¦ m¦ jedinice skale desno ili lijevo duž x-ose i dalje ¦ l¦ jedinice razmjera gore ili dolje duž ose y.

4. Grafičko rješenje kvadratne jednadžbe

Koristeći kvadratnu funkciju kao primjer, razmotrit ćemo grafičko rješenje kvadratne jednadžbe. Graf kvadratne funkcije je parabola.

Šta su stari Grci znali o paraboli?

Savremeni matematički simbolizam nastao je u 16. veku.

Drevni grčki matematičari nisu imali ni koordinatnu metodu ni koncept funkcije. Ipak, oni su detaljno proučavali svojstva parabole. Genijalnost drevnih matematičara jednostavno zadivljuje maštu - na kraju krajeva, mogli su koristiti samo crteže i verbalne opise zavisnosti.

Najpotpunije je istražio parabolu, žirobolu i elipsu Apolonije iz Perge, koji je živio u 3. vijeku prije nove ere. On je tim krivuljama dao imena i naznačio koje uslove ispunjavaju tačke koje leže na ovoj ili onoj krivulji (na kraju krajeva, nije bilo formula!).

Postoji algoritam za konstruisanje parabole:

Pronađite koordinate vrha parabole A (x 0; y 0): X 0 =- b/2 a;

Y 0 = ax o 2 + in 0 + c;

Naći os simetrije parabole (prava x = x 0);

Sastavljamo tablicu vrijednosti za izgradnju kontrolnih tačaka;

Konstruišemo rezultirajuće tačke i konstruišemo tačke koje su im simetrične u odnosu na os simetrije.

1. Koristeći algoritam, konstruisaćemo parabolu y = x 2 - 2 x - 3 . Apscise tačaka preseka sa osom x i postoje korijeni kvadratne jednadžbe x 2 - 2 x - 3 = 0.

Postoji pet načina da se ova jednačina riješi grafički.

2. Podijelimo jednačinu na dvije funkcije: y= x 2 I y= 2 x + 3

3. Podijelimo jednačinu na dvije funkcije: y= x 2 -3 I y =2 x. Korijeni jednadžbe su apscise presječnih tačaka parabole sa pravom linijom.

4. Transformirajte jednačinu x 2 - 2 x - 3 = 0 izolacijom kompletnog kvadrata u funkcije: y= (x -1) 2 I y=4 . Korijeni jednadžbe su apscise presječnih tačaka parabole sa pravom linijom.

5. Podijelite obje strane člana jednačine po članu x 2 - 2 x - 3 = 0 on x, dobijamo x - 2 - 3/ x = 0 , podijelimo ovu jednačinu na dvije funkcije: y = x - 2, y = 3/ x. Korijeni jednadžbe su apscise presječnih tačaka prave i vertikalne krive.

5. Grafičko rješenjezidne jednačinen

Primjer 1. Riješite jednačinu x 5 = 3 - 2 x.

y = x 5 , y = 3 - 2 x.

odgovor: x = 1.

Primjer 2. Riješite jednačinu 3 vx = 10 - x.

Korijeni ove jednadžbe su apscisa točke presjeka grafova dvije funkcije: y = 3 vx, y = 10 - x.

odgovor: x = 8.

- Zaključak -

Nakon što smo pogledali grafikone funkcija: at = sjekira 2 + bx+ c, y =k / x, y = vx, y =|x|, y =x 3 , y =x 4 ,y = 3v x, Primijetio sam da su svi ovi grafikoni izgrađeni po pravilu paralelnog ležaja u odnosu na osi x I y.

Na primjeru rješavanja kvadratne jednačine možemo zaključiti da je grafička metoda primjenjiva i za jednačine stepena n.

Grafičke metode za rješavanje jednačina su lijepe i razumljive, ali ne daju 100% garanciju rješavanja bilo koje jednačine. Apscise presječnih tačaka grafova mogu biti približne.

U 9. razredu i srednjoj školi nastaviću da se upoznajem sa ostalim funkcijama. Zanima me da li se te funkcije pridržavaju pravila paralelnog prijenosa prilikom konstruiranja svojih grafova.

Iduće godine bih takođe želeo da razmotrim pitanja grafičkog rešavanja sistema jednačina i nejednačina.

Književnost

1. Algebra. 7. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

2. Algebra. 8. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

3. Algebra. 9. razred. Dio 1. Udžbenik za obrazovne ustanove / A.G. Mordkovich. M.: Mnemosyne, 2007.

4. Glazer G.I. Istorija matematike u školi. VII-VIII razredi. - M.: Obrazovanje, 1982.

5. Časopis Matematika br. 5 2009; br. 8 2007; br. 23 2008.

6. Web stranice za grafičko rješenje jednačina na Internetu: Tol VIKI; stimul.biz/ru; wiki.iot.ru/images; berdsk.edu; stranica 3-6.htm.

DAGESTANSKI INSTITUT NAPREDNIH PROFESIONALCA

NASTAVNO OSOBLJE

ODSJEK ZA FIZIKU I MATEMATIKU I IKT

Projekt

na temu:

„Izgradnja i reformacija

grafovi funkcija

na školskom kursu matematike »

Rabadanova P.A.

nastavnik matematike

MBOU "Srednja škola Kochubeyskaya"

Tarumovski okrug

2015

1. Uvod………………………………………………………………………….….3

2. Poglavlje I. Pregled literature na temu projekta……………………………..5

3. Poglavlje II. Empirijski dio:

3.1. Osnovne metode za pretvaranje grafova funkcija……….….7

3.2. Zaplet čakIneparne funkcije…………….. 10

3.3. Iscrtavanje grafika inverzne funkcije…………………………………. 11

3.4. Deformacija (kompresija i rastezanje) grafova………………….12

3.5.Kombinacija prijenosa, refleksije i deformacije………..13

4.Zadaci za samostalno rješavanje…………………………………..…...14

5. Zaključak………………………………………………………………………………………………15

6. Zaključci……………………………………………………………………..………17

UVOD

Transformacija grafova funkcija jedan je od temeljnih matematičkih koncepata koji se direktno odnosi na praktične aktivnosti. Grafikoni odražavaju promjenjivost i dinamiku stvarnog svijeta, međusobne odnose stvarnih objekata i pojava.

Funkcionalna linija je osnovna tema koja se obrađuje na Glavnom i Jedinstvenom državnom ispitu.Također, mnogi matematički koncepti se ispituju korištenjem grafičkih metoda. Na primjer, dakvadratnifunkcija se uvodi i proučava u bliskoj vezi sa kvadratnim jednačinama i nejednačinama.Iz toga slijediPodučavanje učenika kako da konstruišu i transformišu grafove funkcija jedan je od glavnih zadataka nastave matematike u školi.

Proučavanje funkcije omogućava pronalaženje odomena definicije i domena vrijednosti funkcije, domenaSmanjenje ili povećanje stope, asimptote, intervaliKonstantnost znakova, itd. Međutim, da se napravi grafmožete koristiti mnoge funkcijekoristiti brojne metodeolakšavajućiizgradnja. Zbog toga studenti moraju imati kompetenciju da konstruišu grafove koristeći metodološke šeme.

Gore navedeno određujerelevantnost istraživačke teme.

Predmet proučavanja je studija transformacije funkcionalnih linijskih grafova u školskoj matematici.

Predmet studija - proces konstruisanja i transformacije grafova funkcija u srednjoj školi.

Svrha studija: edukativna - sastoji se u identifikaciji metodološke šeme za konstruisanje i transformaciju grafova funkcija;razvija - razvoj apstraktnog, algoritamskog, logičkog mišljenja, prostorne mašte;obrazovni – negovanje grafičke kulture školaraca, razvijanje sposobnosti mentalnog rada.

Ciljevi su doveli do sljedeće odlukezadaci:

1. Analizirati edukativne i metodološke materijale o problemu koji se proučava.

2. Identifikujte metodološke šemetransformacija grafova funkcija u školskom kursu matematike.

3. Odaberite najefikasnije metode i sredstvakonstrukcija i transformacija grafova funkcija u srednjoj školi, promicanje: smislenog usvajanja nastavnog materijala; povećanje kognitivne aktivnosti učenika; razvoj njihovih kreativnih sposobnosti.

HIPOTEZA istraživanje: formiranje grafičkih vještina u procesu izučavanja funkcija i njegovanje grafičke kulture učenika efektivno ako učenici znaju metodološku šemu za konstruisanje i transformaciju grafova funkcija u školskom predmetu matematike.

POGLAVLJE I . PREGLED LITERATURE NA TEMU PROJEKTA.

U pripremi projekta proučavali smo sljedeću literaturu:

Sivashinsky, I. Kh. Teoreme i problemi iz algebre, elementarne funkcije - M., 2002. - 115 str.

Gelfand, I. M., Glagoleva, E. G., Šnol, E. E. Funkcije i grafovi (osnovne tehnike) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Osnovna matematika - M., 2010 (reprint). - 590 s.

Kuzmin, M. K. Grafiranje funkcije - J. Matematika u školi. - 2003. - br. 5. - str. 61-62.

Shilov G.E. Kako napraviti grafikone? - M., 1982.

Isaac Thanatar. Geometrijske transformacije grafova funkcija - MCNME, 2012

INPrimjećuje se da se sposobnost „čitanja“ ponašanja funkcije na određenom skupu pomoću grafa koristi ne samo u predmetu matematike, već iu svakoj praktičnoj ljudskoj aktivnosti u kojoj se mora baviti određenim grafičkim prikazima zavisnosti. . Stoga bi učenici trebali biti u stanju da odrede neka od njegovih svojstava iz grafa funkcije.

Teorijski materijal za pretvaranje grafova je striktno predstavljen. Tehnika je praćena ilustracijama, crtežima, primjerima različite složenosti i njihovim rješenjima, što omogućava dubinsko proširivanje znanja i konstruiranje grafova složenih funkcija.

Predstavlja elektronski kurs za obuku, čiji obim i sadržaj odgovara uslovima za srednjoškolski kurs matematike. Teorijski materijal je potkrijepljen grafičkim ilustracijama animacije koje pružaju vizualni prikaz teme koja se proučava. Kurs obuhvata tri modula: modul za proučavanje teorijskog gradiva, modul za samotestiranje i modul za kontrolu znanja.

Za empirijski dio projekta korištene su metodološke sheme za konstruiranje grafova i primjeri za samostalan rad.

Zaključci za Poglavlje 1

Proučavanje nastavne i metodičke literature omogućilo je:

1. Identifikujte metodološku šemuproučavanje, konstruisanje i transformisanje grafova funkcija u školskom predmetu matematike.

2. Odaberite najefikasnije metode i sredstvakonstrukcija i transformacija grafova funkcija u školskoj matematici,doprinoseći:

smisleno učenje obrazovnog materijala;

povećanje kognitivne aktivnosti učenika;

razvoj njihovih kreativnih sposobnosti.

3. pokazati to Funkcijska linija ima značajan uticaj pri učenju različitih pojmova iz matematike.

Poglavlje 2. EMPIRIJSKI DIO

U ovom poglavlju ćemo pogledati glavne metode za transformaciju grafova funkcija i dati metodološke šeme za konstruisanje različitih kombinacija grafova za različite funkcije.

2.1. OSNOVNE METODE ZA TRANSFORMACIJU GRAFIKA FUNKCIJE

Translacija duž ordinatne ose

f ( x ) f ( x )+ b .

Zagrafički prikaz funkcijey = f( x) + bpratećiet:

1. grafikon funkcijey= f( x)

2. pomeriti osuapscisa do| b| jedinice gore nab>0 ili kod| b| jestisedždu nab < 0. Dobija se u novom koor sistemudinat graf je graf funkcijey = f( x) + b.

2. Transfer zajedno sjekire apscisa

f ( x ) f ( x + a ) .

y = f( x+ a) praćenjeet:

3. Iscrtavanje funkcije forme y = f (- x )

f (x ) f (- x ).

Za grafički prikaz funkcijey = f( - x) slijedi:

grafirati funkcijuy = f( x)

odraziti na tou odnosu na y-osu

rezultirajući graf jegraf funkcijey = f( - X).

4. Iscrtavanje funkcije forme y = - f ( x )

f ( x ) - f ( x )

- f( x) slijedi:

grafirati funkcijuy= f( x)

odražavaju ga u odnosu na x-osu

2.2. Zaplet čak I neparne funkcije

Prilikom crtanjaparne i neparne funkcije, zgodno je koristiti sljedeća svojstva:

1. Grafikon funkcije parne simetrijeric u odnosu na ordinatnu osu.

2. Graf neparne funkcije je simetričan u odnosu na ishodište.

Za iscrtavanje grafova parne i neparne funkcije, dovoljno je iscrtati samo desnu granu grafa za pozitivne vrijednosti argumenta. Lijeva grana je završena simetrično u odnosu na ishodište koordinata za neparnu funkciju i u odnosu na os ordinate za parnu funkciju.

Za grafički prikaz parne funkcije y = f ( x ) sljedeći udarci:

izgraditi granu grafa ove funkcije samo u volumenuraspon pozitivnih vrijednosti argumenta x≥O.

Opratiti ovu granu u odnosu na ordinatnu osu

Za grafički prikaz neparne funkcije y = f ( x ) slijedi:

izgraditi granu grafa ove funkcije samo upodručja pozitivnih vrijednosti argumenata (x≥0).

Opratiti ovu granu u odnosu na porijeklou područje negativnih x vrijednosti.

2.3. Grafički prikaz inverzne funkcije

Kao što je već napomenuto, direktna i inverzna funkcija vasodražavaju isti odnos između varijablix i y, sa jedinom razlikom što su u inverznoj funkciji ovivarijable su zamijenile uloge, što je jednako promjenirazumijevanje oznaka koordinatnih osa. Stoga rasporedinverzna funkcija je simetrična grafu direktne funkcijeu odnosu na simetraluIIIIIkoordinatni uglovi,odnosno relativno ravnoy = x. Dakle, dobijamosledeće pravilo.

Za crtanje funkcije y = (x), inverzno funkcijiy = f( x), treba izgraditirasporedy = f( x) i odražavaju ga u odnosu na pravu liniju y = x.

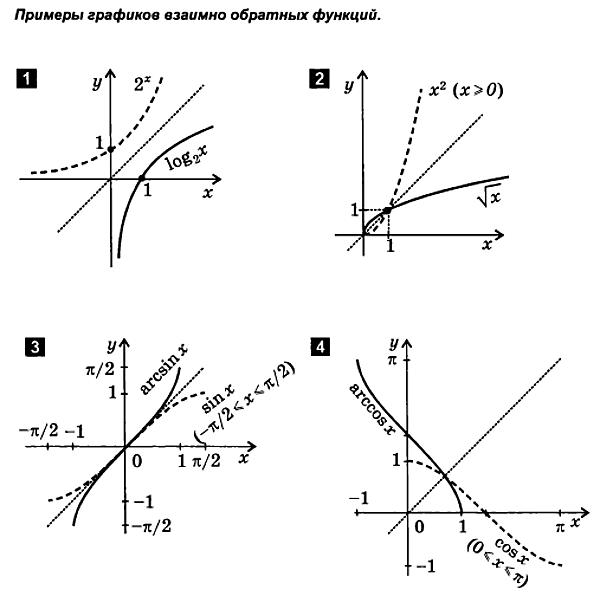
2.4. Deformacija (kompresija i rastezanje) grafova

1. Kompresija (istezanje) grafa duž ordinatne ose

f ( x ) A ∙ f ( x ).

Za grafički prikaz funkcijey= A∙ f( x) slijedi:

8. Kompresija (istezanje) grafika duž x-ose

f( x)

Da se nacrta graf funkcije y= f( x) slijedi:

2.5. Kombinacija transfera, refleksije i warp-a

Vrlo često pri konstruiranju grafova funkcija kadapromijeniti kombinaciju tehnika.

Uzastopna primjena niza ovakvih tehnika držanjaomogućava vam da značajno pojednostavite konstrukciju grafa koristećifunkciju pokretanja i često je smanje na kraju nakonstrukcija jedne od najjednostavnijih elementarnih funkcijacije. Razmotrimo kako, uzimajući u obzir gore navedeno, to slijedigraditi grafove funkcija.

Imajte na umu da je vrijemePreporučljivo je da se dokument pojednostavljenja izvede u sljedećem redoslijeduness.

Koristeći paritet ilineparna funkcija.

Prijenos sjekira.

Refleksija i deformacija.

Konstrukcija grafa se izvodi obrnutim redoslijedom.

Primjer. Grafikujte funkciju

Izvođenje ćemo izvesti u sljedećim koracima:

1. izgraditi graf prirodnog logaritma:

2. stisnutido oseOY2 puta:;
3. prikazati simetričnou odnosu na osuOY: ;
4. kretati se duž oseOXon(!!!) nadesno::

5. prikazati simetrično oko oseOX: ;
6. krenimoduž oseOYdo 3 jedinice::

PRIMJERI KONSTRUKCIJE I TRANSFORMACIJE GRAFIKE FUNKCIJE

Primjer 1. Grafikujte funkciju.

Prvo, nacrtajmo sinusni graf čiji je period jednak:

graf funkcijedobijeno kompresijom grafana ordinatnu osu dva puta. log .

Grafikujte funkcijuat = 2 cosX.

Grafikujte funkcijuy = grijehx .

ZAKLJUČAK

U toku rada na projektu analizirana je različita edukativna i metodička literatura o ovom problemu. Rezultati studije su omogućili da se identifikuju najkarakterističniji pozitivni aspekti studije, konstrukcija i transformacija grafova funkcija u školskom predmetu matematike

Osnovni cilj projekta je razvijanje sposobnosti učenika u čitanju i dovršavanju crteža, te razvijanje racionalnih metoda samostalne aktivnosti kod njih.

Potrebu za unapređenjem grafičkog obrazovanja uopšte diktiraju ne samo savremeni proizvodni zahtevi, već i uloga grafike u razvoju tehničkog mišljenja i kognitivnih sposobnosti učenika. Sposobnost osobe da obrađuje grafičke informacije jedan je od pokazatelja njegovog mentalnog razvoja. Stoga bi grafička obuka trebala postati sastavni element opšteobrazovne obuke.

zaključci

Dakle, razvijeni projekat „Konstrukcija i transformacija grafova funkcija“, posvećen jednom od centralnih pojmova matematike – funkcionalnoj zavisnosti, ima za cilj sistematizaciju i proširenje znanja učenika. Proučavanje specifičnih metoda za transformaciju grafova funkcija vrši se analitički i grafički prema strogim metodološkim shemama. Prikupljeni materijal se može koristiti u nastavi i za samoobuku učenika. Za izvođenje nastave mogu se koristiti različiti oblici i metode organizacije i obuke.

Jedan od načina rješavanja jednačina je grafički. Zasniva se na konstruisanju grafova funkcija i određivanju njihovih presečnih tačaka. Razmotrimo grafičku metodu za rješavanje kvadratne jednačine a*x^2+b*x+c=0.

Prvo rješenje

Hajde da transformišemo jednačinu a*x^2+b*x+c=0 u oblik a*x^2 =-b*x-c. Gradimo grafove dvije funkcije y= a*x^2 (parabola) i y=-b*x-c (prava). Tražimo raskrsnice. Apscise presječnih tačaka će biti rješenje jednačine.

Pokažimo na primjeru: riješiti jednačinu x^2-2*x-3=0.

Hajde da ga transformišemo u x^2 =2*x+3. Konstruišemo grafove funkcija y= x^2 i y=2*x+3 u jednom koordinatnom sistemu.

Grafovi se sijeku u dvije tačke. Njihove apscise će biti korijeni naše jednadžbe.

Rješenje po formuli

Da bismo bili uvjerljiviji, hajde da analitički provjerimo ovo rješenje. Rešimo kvadratnu jednačinu koristeći formulu:

D = 4-4*1*(-3) = 16.

X1= (2+4)/2*1 = 3.

X2 = (2-4)/2*1 = -1.

znači, rješenja su ista.

Grafička metoda rješavanja jednačina također ima svoj nedostatak, uz njegovu pomoć nije uvijek moguće dobiti točno rješenje jednačine. Pokušajmo riješiti jednačinu x^2=3+x.

Konstruirajmo parabolu y=x^2 i pravu liniju y=3+x u jednom koordinatnom sistemu.

Opet smo dobili sličan crtež. Prava linija i parabola seku se u dve tačke. Ali ne možemo reći tačne vrijednosti apscisa ovih tačaka, samo približne: x≈-1,3 x≈2,3.

Ako smo zadovoljni odgovorima takve tačnosti, onda možemo koristiti ovu metodu, ali to se rijetko događa. Obično su potrebna tačna rješenja. Stoga se grafička metoda rijetko koristi, i to uglavnom za provjeru postojećih rješenja.